[BOJ] 2261번: 가장 가까운 두 점

문제 링크: https://www.acmicpc.net/problem/2261

문제 상황

2차원 평면상의 \(n\)개의 점이 주어질때, 각 점들간 거리 중 가장 작은 값을 구하라.

입력

Line 1: 자연수 \(n (2≤n≤100,000)\) Line 2~(\(n+1\)): \(x_i\), \(y_i\) (각 점의 x, y좌표)

ex)

출력

각 점들간 거리 중 최소 값을 그 제곱으로 출력.

ex)

1. 무식하게 시도하기

이번에는 무려 Platinum III 문제다.

당연히 시간초과가 나겠지만 한번 무식하게 일일히 하나하나 탐색하는 방법을 시도하였다.

C++17로 구현하였다.

#include <iostream>
#include <vector>

using namespace std;

class Pos{
    private:
        int x, y;
    public:
        Pos(){ cin>>x; cin>>y; }
        Pos(int x, int y): x(x),y(y) {}
        bool operator!=(Pos other){ return !(x==other.x&&y==other.y); }
        int dist_sqr(Pos other){
            return (x-other.x)*(x-other.x)+(y-other.y)*(y-other.y);
        }
};

int main(int argc, const char *argv[]){
    ios::sync_with_stdio(false);
    cin.tie(NULL); cout.tie(NULL);

    int n, ans=800000000; // MAX_VALUE:800,000,000 (max distance: 10000×2×√2)
    cin>>n;

    vector<Pos> v;
    v.reserve(n);

    for(int i=0; i<n; ++i){
        v.push_back(Pos());
        vector<Pos>::iterator curr = v.end()-1;
        for(vector<Pos>::iterator it=v.begin();it!=curr;++it)
            ans=min(ans,curr->dist_sqr(*it));
    }

    cout<<ans;
    return 0;
}

결과	메모리	시간	코드 길이
`시간초과`			863B

제출 소스 확인하기

당연한 결과가 나왔다. \(n\)개의 점이 있을경우 이 점을 모두 선분으로 이을 때 그 선분의 수는 \(_nC_2\)와 같다. 즉 \(\frac{n(n-1)}{2}\)이니 시간복잡도는 \(O(n^2)\)이다. 집어치우자.

2. Divide and Conquer

‘분할 정복’ 단계 분류를 들어가보면 무려

가장 가까운 두 점을 구하는 문제. 잘 알려진 문제지만 상당히 어렵기 때문에 검색을 추천드립니다.

와 같이 설명되어 있다.

선형적인 구조라면 뭐라도 해볼 거 같은데 평면구조라니 뭘 어찌해야할지 모르겠다… 물론 분류가 분할정복이니 분할정복으로 접근해야겠지만 그조차도 어떻게 접근해야할지 잘 모르겠다.

2-1. 검색

역시 검색하면 잘 나온다. 검색어: BOJ 2261

Casterian님의 블로그 글을 참고하였다.

\(y\) 축과 나란하게 직선을 그어서 평면을 둘로 나눕시다. 모든 점을 \(x\) 좌표 기준으로 정렬한 다음 \(\frac{n}{2}\)번째와 \(\frac{n}{2}+1\)번째 점의 \(x\) 좌표 평균을 기준 직선으로 잡겠습니다.

사실 분할하는거 보면 그리 특별할게 없다.

2-2. 문제해결 전략

위 블로그 게시글을 이어서 계속 요약해보았다.

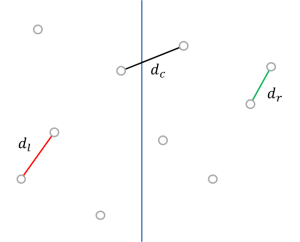
이처럼 분할하면 문제는 총 세 가지 경우로 나뉘는데,

두 점 모두 왼쪽에 속할 경우 (\(d_l\))
두 점 모두 오른쪽에 속할 경우 (\(d_r\))
양쪽에서 한 점씩 나오는 경우 (\(d_c\))

각 경우에 대해서 최솟값을 구한 다음 이 중 최소값을 구하면 되겠다.

1번과 2번은 재귀적으로 해결할 수 있지만, 3번은 왼쪽에 \(\frac{n}{2}\)개, 오른쪽에 \(\frac{n}{2}\)개중 양쪽에서 하나씩 뽑아 비교해야겠다. 총 \(\frac{n^2}{4}\)가지 경우가 있고, 모든 경우에 대해 다 길이를 계산한 다음 그 최솟값을 찾게되면 시간복잡도 \(T(n)\)은

\[T(n)=2T(\frac{n}{2})+O(n^2)\]

이며 마스터 정리에 따라 결국 \(T(n)=O(n^2)\)이다. 3번 경우를 해결하지 않는 한 시간복잡도가 낮아지지 않는다.

2-3. 시간복잡도 줄이기: 서로 다른 분할구간에 걸친 경우

결국 꼼수를 써서 답이 될 수 없는 후보들을 걸러내는 작업을 통해 후보군을 줄여야 계산 양이 줄어들 것이다. 1, 2번 경우를 계산하여 특정 값\((d=min(d_l,d_r))\)이 나왔다면 3번경우에서 이 특정값 \(d\)보다 큰 값은 어차피 답이 아니니 이를 걸러낼 방법을 찾아야 한다.

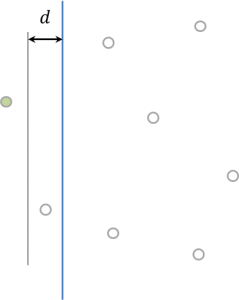
우리는 3번경우 ‘분할선 기준 양쪽에서 한 점씩 나오는 경우’를 계산하고 있음에 주목하라. 때문에 분할선 기준으로 1, 2번에서 찾은 최소값 \(d\)보다 멀리 떨어진 점들은 후보가 될 수 없다.

여기에 한 술 더 떠서 앞서 추린 후보군들을 \(y\)좌표 기준으로 다시 정렬해 또 \(d\)보다 먼 점들을 제외시킬 수 있다. 중복을 피하기 위해서 이번엔 비교 방법을 조금 바꾸어 제일 아래에 있는 점부터 시작해서 각 점을 자기보다 더 위에 있는 점(\(y\)좌표가 자기와 같거나 더 큰 점)이랑만 비교한다.

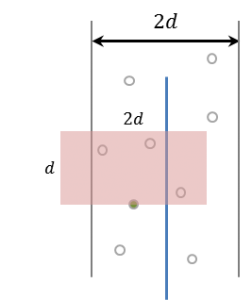
결론적으로 y좌표 기준으로 정렬한 뒤 각 점을 자기보다 y좌표가 같거나 높은 것들을 비교하다가 y좌표 차가 d 이상이 되면 그 점에 대한 비교를 끝내면 됩니다. 그렇다면 문제는 비교가 최대 몇 번이냐는 건데, 절대 7번을 넘지 않습니다. 증명 ~~이왜진…?~~

뭐 증명이 그렇다니까…

쨌든 이렇게 3번경우를 계산하게되면, \(y\)좌표 기준 정렬에 \(O(n\ log\ n)\), 그리고 추려낸 점 최대 \(n\)개에 대해 각 점을 최대 점 7개와 비교하는데 \(O(n)\) 이 되므로, 3번경우 계산을 \(O(n\ log\ n)\)으로 단축시켰다.

따라서 이때 전체 계산과정의 시간복잡도 \(T(n)\)은

\[T(n)=2T(\frac{n}{2})+O(n\ log\ n)\]

이 되며, 마스터 정리에 따라 결국 \(T(n)=O(n\ log^2\ n)\)이 된다.

2-4. 구현하기

2-4-1. 입출력 환경 및 좌표 구현

우선 분할정복으로 계산하는 부분을 빼고 나머지를 구현해보자. 특별한 탐색이 필요하지 않을 것으로 보여 가장 기본적인 자료구조인 vector에 좌표를 저장하기로 했다. pair를 써도 되겠지만, 좌표 정렬 및 거리계산등의 기능을 생각하면 따로 클래스를 구현하는게 유리하겠다.

#include <iostream>
#include <vector>

using namespace std;

class Pos{
    public:
        int x, y;
        Pos(){ cin>>x; cin>>y; }
        Pos(int x, int y): x(x),y(y) {}
        bool operator!=(Pos other){ return !(x==other.x&&y==other.y); }
        bool operator<(Pos other){ return (x!=other.x?x<other.x:y<other.y); }
};
int dist_sqr(Pos& a, Pos& b){
    return (a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y);
}
int solve(vector<Pos> v){
    int d=0;
    // Process Somehow
    return d;
}

int main(int argc, const char *argv[]){
    ios::sync_with_stdio(false);
    cin.tie(NULL); cout.tie(NULL);

    int n;
    cin>>n;

    vector<Pos> v;
    v.reserve(n);

    for(int i=0; i<n; ++i)
        v.push_back(Pos());

    cout<<solve(v);
    return 0;
}

2-4-2. 분할 구현

앞서 다음과 같은 분할방법을 언급했었다.

두 점 모두 왼쪽에 속할 경우 (\(d_l\))

두 점 모두 오른쪽에 속할 경우 (\(d_r\))

양쪽에서 한 점씩 나오는 경우 (\(d_c\))

영역을 분할할 적절한 선을 지정 후, 두 영역으로 분할하며, 정복하는 과정에서는 두 영역에서의 값과 양쪽에서 한 점씩 골랐을때 최소값을 비교한다.

int midLine(Pos& a, Pos& b){ return (a.x+b.x)>>1; }

int solve(vector<Pos>::iterator it, int n){
    if(n==2) return dist_sqr(it[0],it[1]);
    if(n==3) return min(dist_sqr(it[0],it[1]),dist_sqr(it[1],it[2]));

    int line = midLine(it[n/2-1],it[n/2]);
    int d = min(solve(it,n>>1),solve(it+(n>>1),n-(n>>1)));

    for(int i=0; i<line; ++i)
        for(int j=line; j<n; ++j)
            d = min(d,dist_sqr(mid[i],mid[j]));
    
    return d;
}

위에서 구현한 코드는 x좌표에 대해 오름차순으로 정렬되어 있다는 전제하에 구현되었다. 미리 정렬해 놓으면 매번 비교할 필요가 없다.

때문에 아래와 같이 solve호출 전 sort함수를 통해 미리 정렬해주자. sort함수 사용을 위해 #include <algorithm>이 필요함에 유의하라.

#include <iostream>
#include <algorithm> // for sort algorithm
#include <vector>

...

int main(int argc, const char *argv[]){

    ...

    vector<Pos> v;
    v.reserve(n);

    for(int i=0; i<n; ++i)
        v.push_back(Pos());

    sort(v.begin(),v.end());

    cout<<solve(v.begin(),n);
    return 0;
}

2-4-3. 후보 추리기

분할선 기준으로 1, 2번에서 찾은 최소값 \(d\)보다 멀리 떨어진 점들은 후보가 될 수 없다.

여기에 한 술 더 떠서 앞서 추린 후보군들을 \(y\)좌표 기준으로 다시 정렬해 또 \(d\)보다 먼 점들을 제외시킬 수 있다.

앞서 ‘두 점이 분할된 두 영역에 하나씩 위치한 경우’의 계산을 위와 같은 방법으로 개선할 수 있음을 다루었다.

int midLine(Pos& a, Pos& b){ return (a.x+b.x)>>1; }
bool ascendY(Pos& a, Pos& b){ return (a.y!=b.y?a.y<b.y:a.x<b.x); }

int solve(vector<Pos>::iterator it, int n){
    if(n==2) return dist_sqr(it[0],it[1]);
    if(n==3) return min(dist_sqr(it[0],it[1]),dist_sqr(it[1],it[2]));

    int line = midLine(it[n/2-1],it[n/2]);
    int d = min(solve(it,n>>1),solve(it+(n>>1),n-(n>>1)));

    vector<Pos> mid;
    for(int i=0; i<n; ++i){
        int temp = line-it[i].x;
        if(d>temp*temp)
            mid.push_back(it[i]);
    }
    sort(mid.begin(),mid.end(),ascendY);

    int midSiz = mid.size();
    for(int i=0; i<midSiz; ++i)
        for(int j=i+1; j<midSiz&&((mid[j].y-mid[i].y)*(mid[j].y-mid[i].y)<d); ++j)
            d = min(d,dist_sqr(mid[i],mid[j]));
    
    return d;
}

분할정복을 구현할때는 언제나 분할을 중단하는 지점을 설정하고, 처리하여야 함을 잊지말자.

또한 앞서 구한 최소값보다 멀리 떨어져 있음이 확실한 점들은 제외하여 후보를 추려낸 후, 이들을 y좌표에 대한 오름차순으로 다시 정렬하여 계산 및 비교 작업을 하도록 구현하였다.

2-5. 최종코드

#include <iostream>
#include <algorithm>
#include <vector>

using namespace std;

class Pos{
    public:
        int x, y;
        Pos(){ cin>>x; cin>>y; }
        Pos(int x, int y): x(x),y(y) {}
        bool operator!=(Pos other){ return !(x==other.x&&y==other.y); }
        bool operator<(Pos other){ return (x!=other.x?x<other.x:y<other.y); }
};
int dist_sqr(Pos& a, Pos& b){
    return (a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y);
}
int midLine(Pos& a, Pos& b){ return (a.x+b.x)>>1; }
bool ascendY(Pos& a, Pos& b){ return (a.y!=b.y?a.y<b.y:a.x<b.x); }

int solve(vector<Pos>::iterator it, int n){
    if(n==2) return dist_sqr(it[0],it[1]);
    if(n==3) return min(dist_sqr(it[0],it[1]),dist_sqr(it[1],it[2]));

    int line = midLine(it[n/2-1],it[n/2]);
    int d = min(solve(it,n>>1),solve(it+(n>>1),n-(n>>1)));

    vector<Pos> mid;
    for(int i=0; i<n; ++i){
        int temp = line-it[i].x;
        if(d>temp*temp)
            mid.push_back(it[i]);
    }
    sort(mid.begin(),mid.end(),ascendY);

    int midSiz = mid.size();
    for(int i=0; i<midSiz; ++i)
        for(int j=i+1; j<midSiz&&((mid[j].y-mid[i].y)*(mid[j].y-mid[i].y)<d); ++j)
            d = min(d,dist_sqr(mid[i],mid[j]));
    
    return d;
}

int main(int argc, const char *argv[]){
    ios::sync_with_stdio(false);
    cin.tie(NULL); cout.tie(NULL);

    int n;
    cin>>n;

    vector<Pos> v;
    v.reserve(n);

    for(int i=0; i<n; ++i)
        v.push_back(Pos());

    sort(v.begin(),v.end());

    cout<<solve(v.begin(),n);
    return 0;
}

결과	메모리	시간	코드 길이
`맞았습니다!!`	3440KB	80ms	1518B

제출 소스 확인하기

PREVIOUS6549번: Largest Rectangle in a Histogram