문제 링크: https://www.acmicpc.net/problem/2447
문제 상황
- \(1≤k<8\)을 만족하는 정수 \(k\)에 대해, \(N=3^k\)이다.
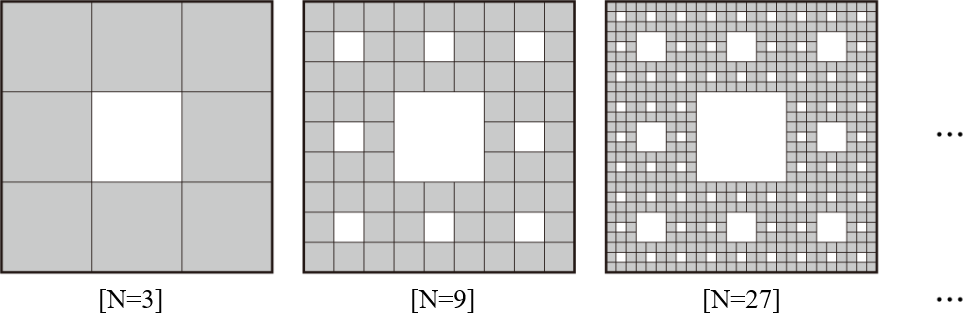
- 위와 같은 \(N\)에 대해 \(N×N\) 크기의 ‘*’ 과 ‘ ‘ 로 이루어진 패턴은 다음과 같이 귀납적으로 정의된다.
- \(N>3\)일때, N크기의 패턴은 가운데 \((N÷3)×(N÷3)\) 크기 공백의 정사각형을 \((N÷3)\) 크기의 패턴이 둘러싼 형태이다.
- 크기 3의 패턴은 다음과 같이 정의된다.
N=3 N=9의 패턴
*** *********
* * * ** ** *
*** *********
*** ***
* * * *
*** ***
*********
* ** ** *
*********
입력
첫째 줄에 \(N\)이 주어진다.
출력
첫째줄부터 \(N\)번째 줄까지 문제의 조건에 맞는 패턴의 ‘*’ 을 출력한다.
C11로 구현하였다.
1. 입출력 및 데이터 저장 공간
문제의 패턴은 2차원 형태로 저장되므로 행과 열 정보(인덱스)로 접근하기 용이한 2차원 배열 형태로 저장한다. 입력에 따라 사이즈가 가변적이므로 동적 메모리 할당을 이용해 구현하자.
char** table; // N×N 사이즈 패턴을 저장할 공간을 할당할 2차원 포인터
int N;
scanf("%d",&N);
table=(char**)malloc(N*sizeof(char*));
table[0]=(char*)malloc(N*N*sizeof(char));
// 메모리 할당 효율성과 2차원 배열의 속성을 유지하기 위해 모든 요소를 연속된 공간에 할당한다.
memset(table[0],'*',N*N*sizeof(char));
// memset으로 모든 요소를 '*'로 초기화시켰다. 패턴 규칙에 따라 공백만 바꾸어주면 된다.
for(int row=0;row<N;++row)
table[row]=table[0]+row*N; // 행index×행size = table시작주소로부터의 i행 시작의 상대 주소값
... /*처리 구현*/
for(int row=0;row<N;++row){
for(int col=0;col<N;++col)
putchar(table[row][col]); // '*'이나 ' ' 출력
putchar('\n'); // 행간 개행문자 '\n'
}
free(table[0]); free(table); // 위와 같이 할당 시 할당 해제도 간단하다.
2. 귀납적으로 정의된 패턴 구현 : 재귀적 처리
N크기의 패턴은 가운데 \((N÷3)×(N÷3)\) 크기 공백의 정사각형을 \((N÷3)\) 크기의 패턴이 둘러싼 형태이다.
위와 같이 패턴이 귀납적으로 정의되어서, N크기의 패턴을 구현하려면 해당 영역을 \((N÷3)×(N÷3)\) 크기의 9개 영역으로 분할하여 각 영역을 처리해야 한다. 특정 영역을 나타내는 인덱스를 매개변수로 하는 함수를 선언하고 N이 3 이상이면 9분할된 영역에 대해 자기 자신을 다시 호출하는 재귀함수를 작성해보자.
문제의 패턴도 프랙탈 구조의 일종이므로 함수 이름을 fractal로 정했다.
패턴을 담은 공간을 접근하기 위해 char** table을 우선 인자로 받아야 한다.
영역은 정사각형 형태이기 때문에 위치를 특정할 인자 2개, 크기를 특정할 인자 1개, 총 3개의 인자로 충분히 특정할 수 있다. 편의를 위해 영역의 시작위치의 행 index을 row로, 열 index을 col로 받기로 하였고, 영역의 크기를 n으로 받았다.
void fractal(char** table, int n, int row, int col){
n/=3;
/*중앙 영역 공백 처리 작업*/
if(n==1) return;
fractal(table,n,row,col); fractal(table,n,row,col+n); fractal(table,n,row,col+2*n);
fractal(table,n,row+n,col); /*중앙은 패턴처리가 필요 없다.*/ fractal(table,n,row+n,col+2*n);
fractal(table,n,row+2*n,col); fractal(table,n,row+2*n,col+n); fractal(table,n,row+2*n,col+2*n);
}
영역의 크기로 n을 인자로 받지만, 영역을 9분할 하면서 n을 3으로 나누어 사용할 일이 많기 때문에 매번 3으로 나누는 연산을 하는 대신 함수 시작부터 n을 3으로 나누어 주었다.
n=1의 패턴은 정의되지 않으므로 중앙영역을 공백으로 만든 후 재귀호출 없이 반환할 수 있도록 한다.
이로써 9분할 된 영역중 중앙을 제외한 8개 영역을 위와 같이 호출할 수 있게 되면서, 재귀적으로 패턴을 처리할 수 있게 되었다.
3. 중앙 영역 공백 처리 작업
memset(table[0],'*',N*N*sizeof(char));
// memset으로 모든 요소를 '*'로 초기화시켰다. 패턴 규칙에 따라 공백만 바꾸어주면 된다.
앞서 데이터 저장공간을 위와 같이 ‘*‘로 초기화 했었다. 또한 이전단계에서 fractal 함수를 재귀적으로 호출하여 중앙 영역을 둘러싼 8개 영역이 자기유사성을 가진 패턴이 되도록 처리 할 수 있었다. 따라서 이번 단계에선 해결되지 않은 중앙 영역을 처리해야한다. 패턴의 정의에 따라 단순히 중앙영역을 모두 공백문자 ‘ ‘로 바꾸면 된다.
void fractal(char** table, int n, int row, int col){
n/=3;
for(int i=row+n;i<row+2*n;++i)
for(int j=col+n;j<col+2*n;++j)
table[i][j]=' ';
.../*재귀 호출*/
}
2단계에서 언급하였지만 9분할 때문에 n을 3으로 나눈 값을 계속 사용하므로 n을 3으로 미리 나누어 준 후, 중앙 영역의 경우 행 index는 \([row+n,row+2n-1]\), 열 index는 \([col+n,col+2n-1]\) 이므로 이 구간을 탐색하며 모든 원소를 공백문자 ‘ ‘로 바꿔준다. 이렇게 중앙 영역을 완벽히 공백으로 치환하고, 8개 영역을 재귀호출로 패턴처리하면 9개 영역이 완벽히 처리된다.
4. 최종 코드
앞선 단계에서 구현한 것들을 종합해보자.
#include <stdio.h>
#include <malloc.h>
#include <memory.h>
void fractal(char** table, int n, int row, int col){
n/=3;
for(int i=row+n;i<row+2*n;++i)
for(int j=col+n;j<col+2*n;++j)
table[i][j]=' ';
if(n==1) return;
fractal(table,n,row,col); fractal(table,n,row,col+n); fractal(table,n,row,col+2*n);
fractal(table,n,row+n,col); /*No processing for center area*/ fractal(table,n,row+n,col+2*n);
fractal(table,n,row+2*n,col); fractal(table,n,row+2*n,col+n); fractal(table,n,row+2*n,col+2*n);
}
int main(void){
char** table; int N;
scanf("%d",&N);
table=(char**)malloc(N*sizeof(char*));
table[0]=(char*)malloc(N*N*sizeof(char));
memset(table[0],'*',N*N*sizeof(char));
for(int row=0;row<N;++row)
table[row]=table[0]+row*N;
fractal(table,N,0,0);
for(int row=0;row<N;++row){
for(int col=0;col<N;++col)
putchar(table[row][col]);
putchar('\n');
}
free(table[0]); free(table);
return 0;
}
| 결과 | 메모리 | 시간 | 코드 길이 |
|---|---|---|---|
맞았습니다!! |
5788KB | 88ms | 1009B |
