문제 링크: https://www.acmicpc.net/problem/1931

문제 상황

[Activity-Selection Problem]

• 한개의 회의실에서 열 N개의 회의의 시작, 종료 시각이 주어진다.
• 회의는 한번 시작하면 중간에 중단될 수 없으며, 각 회의가 겹쳐서 열릴 수 없다. (한 회의가 끝나는 것과 동시에 다음 회의가 시작될 수 있다.)
• 회의의 시작시간과 끝나는 시간이 같을 수도 있다. (시작하자마자 끝나는 것)

입력

Line 1: 회의의 수 \(N (1 ≤ N ≤ 100,000)\)

Line 2~(N+1): 각 회의의 정보가 ((시작시각)(공백)(종료시각))의 형태로 주어진다. (시작시각과 종료시각은 \(2^{31}-1\)보다 작은 자연수이거나 \(0\)이다. )

출력

최대 사용할 수 있는 회의의 최대 개수

1. 예시 연구

BOJ 1931에서는 아래와 같은 입력 예시를 제시했다. 아래 예시를 연구하면서 문제 해결 전략을 찾아보자.

입력
11
1 4
3 5
0 6
5 7
3 8
5 9
6 10
8 11
8 12
2 13
12 14

출력
4

힌트
(1,4), (5,7), (8,11), (12,14) 를 이용할 수 있다.

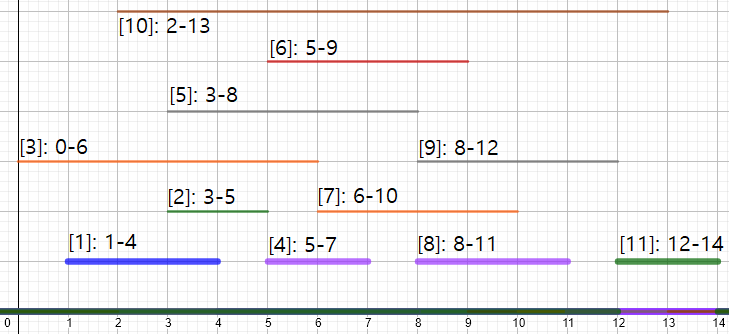
직접 그려보았다. 사실 예시 케이스는 회의 수가 11개 뿐이니 몇 번 시도만으로 4번이 최대임을 알 것 같긴 한데, 회의 수가 최대인 10만개가 나온다하면 머리가 하얘진다. 내가 그걸 계산하지 않더라도 컴퓨터로 계산하면… 거의 모든 경우의 수를 탐색하게 될거고, 탐색하다 ‘이게 아닌가벼’하며 다시 돌아가는 과정을 반복하면 시간복잡도가 \(O(n^2)\)은 되지 않을까 싶다.

우선 위 그림과 같이 시각화를 해봤을때(덕분에 이미 답이 보이지만) 길쭉한건 뭔가 거슬리고 상당히 방해되는 듯 하다. 당연하게도 길다는 건 점유시간이 길다는 뜻이니 회전율이 떨어지고 다른 회의를 열기 어렵다.

그렇다고 점유시간이 짧은 순서대로 정렬하여 차례대로 꺼내쓸 수는 없는 노릇이다. 각각의 회의시간이 어떻게 분포되어 있을 줄 알고…

어쨌든 모든 경우의 수를 탐색하는 건 불가능해보이고, 무작정 점유시간으로 정렬할 수는 없다. 시작 시각이나 종료시각으로 정렬해볼까?

1. 시작시각을 기준으로 (같은경우 종료시각을 기준으로) 오름차순으로 정렬 후 탐색 같은 시작시각을 가진 회의들 중 가장 빨리 끝나는 회의를 찾는다. 그래야 그 다음 회의를 빨리 시작하고 더 많은 회의를 열 수 있다.

2. 종료시각을 기준으로 (같은경우 시작시각을 기준으로) 오름차순으로 정렬 후 탐색 앞서 말한대로 빨리 끝내야 더 많은 기회를 잡는다. 우선 가장 빨리 끝나는거 하나 무조건 열고, 그 다음 가장 빨리 끝나는 회의가 열릴 수 있는지 (회의 시간이 겹쳐서 못 열지 않는지) 탐색해나간다.

둘다 거진 그럴싸해보인다. 시간복잡도가 \(O(n)\)으로 해결 될 것 같다.

2. 전략 구현

C++17로 구현하였다. 이번만 특별히 C++로 구현한 이유는 없다. 그냥 해봤다.

어쨌든, 앞서 이야기 해본 전략을 구현해보자. 우선 입출력, 데이터 저장부터 정하자.

2-1. 입출력 및 데이터 저장

#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;

bool compare(pair<int,int>& a, pair<int,int>& b){
    return /*return result of comparison of a and b*/;
}

int main(int argc, const char * argv[]){
    int N;
    vector<pair<int,int>> v;
    
    for(cin>>N;N;--N){
        int start,finish;
        cin>>start>>finish;
        v.push_back(make_pair(start,finish));
    }
    sort(v.begin(),v.end(),compare);
    
    int cnt=0,time=0;
    for(vector<pair<int,int>>::iterator it=v.begin();it!=v.end();++it){
        /*determine which conference to held*/
    }
    
    cout<<cnt;
    return 0;
}

깔끔하다.

2-2. 시작시각을 기준으로 오름차순으로 정렬 후 탐색

bool compare(pair<int,int>& a, pair<int,int>& b){
    return (a.first!=b.first ? (a.first<b.first) : (a.second<b.second));
}

int cnt=0,time=0;
for(vector<pair<int,int>>::iterator it=v.begin();it!=v.end();++cnt){
    time=it->second;
    while((it++)->first<time);
}

나름 앞선 단계에서 언급한 방식대로 구현해보았다. 그런데 앞서 든 예시를 막상 이렇게 탐색하다보면 [3]: 0-6 을 피할 수 없다. 그 사이에 [1]: 1-4 를 끝내고 [4]: 5-7 을 시작할 수 있는데… 확실히 잘못되었다.

2-3. 종료시각을 기준으로 오름차순으로 정렬 후 탐색

bool compare(pair<int,int>& a, pair<int,int>& b){
    return (a.second!=b.second ? (a.second<b.second) : (a.first<b.first));
}

int cnt=0,time=0;
for(vector<pair<int,int>>::iterator it=v.begin();it!=v.end();++it){
    if(it->first>=time){
        time=it->second;
        ++cnt;
    }
}

예시로 든 케이스는 잘 찾아낸다. 사실 곰곰히 생각해보면 빨리 끝나는 회의 (종료시간이 빠른 회의)을 찾아 먼저 열고 끝내는 것은 ‘횟수’가 하나 늘어난다는 측면에서 다른 회의를 여는 것과 같은 효과를 내면서도 빨리 끝내고 더 많은 시간을 확보하여 다른 회의를 더 열 수 있는 기회를 확보하는 것이다.

3. Activity-Selection Problem

교실할당(classroom assignment)으로도 불리는 문제로, Greedy Algorithm의 대표적인 예시이다. 앞서 이런 말을 했는데,

빨리 끝나는 회의 (종료시간이 빠른 회의)을 찾아 먼저 열고 끝내는 것은 ‘횟수’가 하나 늘어난다는 측면에서 다른 회의를 여는 것과 같은 효과를 내면서도 빨리 끝내고 더 많은 시간을 확보하여 다른 회의를 더 열 수 있는 기회를 확보하는 것이다.

상당히 Greedy Algorithm 답다. 탐욕적이다(?) 아래는 Greedy Algorithm을 이용해 Activity Selection Problem을 푸는 의사코드이다.

Greedy-Iterative-Activity-Selector(A, s, f): 

    Sort A by finish times stored in 
    S = {A[1]} 
    k = 1
    
    n = A.length
    
    for i = 2 to n:
        if s[i] ≥ f[k]: 
            S = S U {A[i]}
            k = i
    
    return S

뭐 앞선 단계에서 구현한 것과 크게 다르지 않아 보인다. Greedy Algorithm을 이미 다룬 적이 있고, Activity-Selection Problem도 이미 위에서 다 구현했고, 딱히 더 설명할 것이 남아 있지 않다.

4. 최종 코드

이제 나누어 구현했던 두가지를 잘 합쳐보자.

#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;

bool compare(pair<int,int>& a, pair<int,int>& b){
    return (a.second!=b.second ? (a.second<b.second) : (a.first<b.first));
}

int main(int argc, const char * argv[]){
    int N;
    vector<pair<int,int>> v;
    
    for(cin>>N;N;--N){
        int start,finish;
        cin>>start>>finish;
        v.push_back(make_pair(start,finish));
    }
    sort(v.begin(),v.end(),compare);
    
    int cnt=0,time=0;
    for(vector<pair<int,int>>::iterator it=v.begin();it!=v.end();++it){
        if(it->first>=time){
            time=it->second;
            ++cnt;
        }
    }
    
    cout<<cnt;
    return 0;
}

제출 소스 확인하기