문제 링크: https://www.acmicpc.net/problem/11729

문제 상황

• 세 개의 장대가 있고, 첫번째 장대에 서로 다른 반경의 원판 n개가 쌓여있다.
• 다음 규칙에 따라 첫번째 장대에 있는 원판들을 모두 세번째 장대로 옮긴다.
  1. 한 번에 한 개의 원판만을 다른 탑으로 옮길 수 있다.
  2. 쌓아 놓은 원판은 항상 위의 것이 아래의 것보다 작아야 한다.
• 이동 순서를 출력한다.

입력

첫 번째 장대에 쌓인 원판의 개수 \(N (1≤N≤20)\)이 주어진다.

출력

Line1: 옮긴 횟수 \(K\) 출력

Line2~(K+1): 정수 A B (A번째 막대의 가장 위에 있는 원판을 B번째 막대로 옮기는 이동 표현)

C99로 구현하였다.

1. 하노이 탑 최소 이동 전략

편의상 원판1, 원판2, 원판3은 각각 첫번째로 작은 원판, 두번째로 작은 원판, 세번째로 작은 원판을 의미한다. 원판의 개수 \(N\)이 \(3\)인 작은 경우를 살펴보며 전략을 찾아내자.

위는 \(N=3\)인 경우 시작하기 전의 그림이다. 각 장대는 스택과 같이 LIFO이기 때문에 가장 위에 쌓인, 가장 작은 원판부터 옮길 수 있다. 또한 세번째 막대로 완전히 옮기려면, 가장 큰 원판3부터 원판2, 원판1 순서로 쌓아야 한다.

그렇다면 원판 3을 장대 1에서 3으로 옮길 수 있도록, 장대 1에는 원판 3만 남기고 장대 3을 비워두도록 하자. 즉 원판 1, 2를 장대 2로 옮겨야 한다.

원판 1을 장대 1에서 3으로 옮겼다. 원판 1을 옮기므로서 원판 2를 움직일 수 있게되었다. 원판 n을 옮기기 위해서 목표지점 외 다른 곳에 원판 n-1을 옮겨 놓아야 한다.

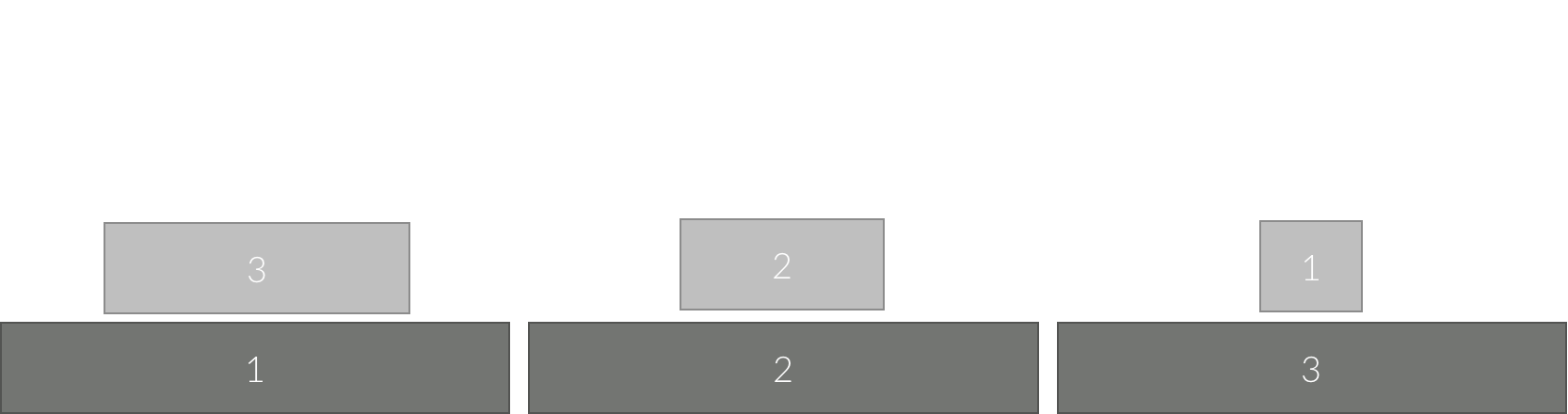
원판 2를 장대 1에서 장대 2로 옮겼다.

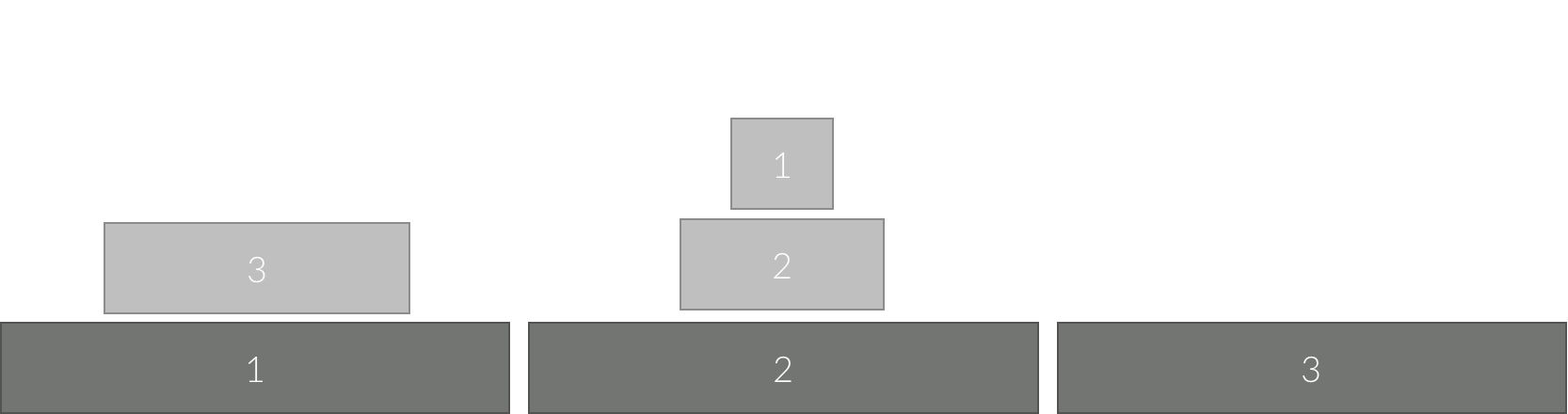
원판 1을 장대 3에서 장대 2로 옮겼다. 비로소 원판 3을 움직일 수 있게되었다. 장대 2의 경우 이미 가장 위에 원판 3보다 작은 원판이 있기 때문에 원판 3을 옮길 수 없고, 장대 3으로만 옮길 수 있다. 때문에 원판 3을 목표지점으로 옮기기 위해 3보다 작은 모든 원판들을 목표지점이 아닌 곳으로 옮기는 작업을 해야한다.

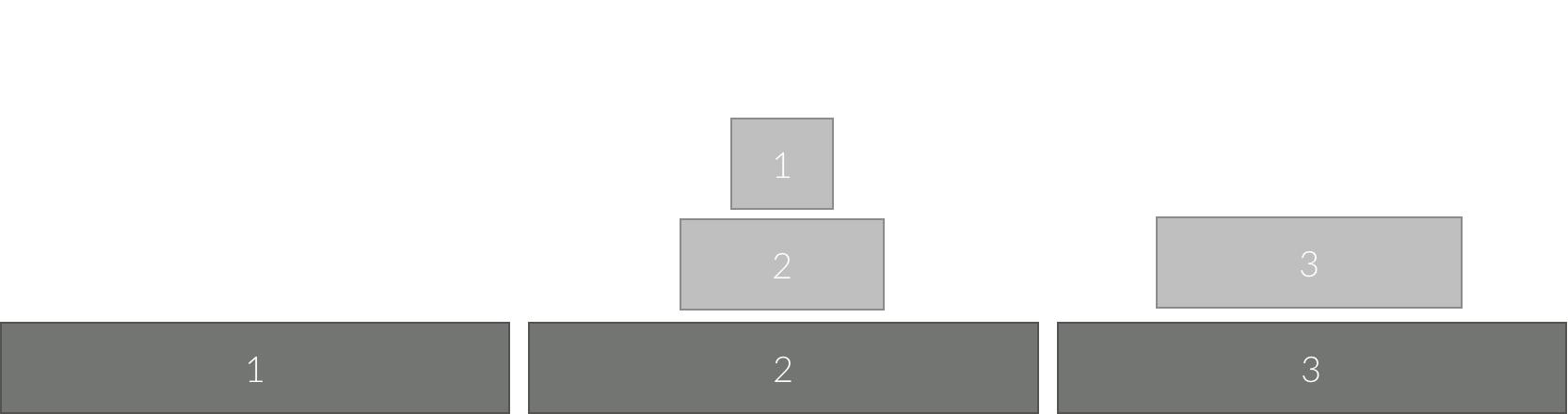
원판 3을 장대 1에서 3으로 옮겼다.

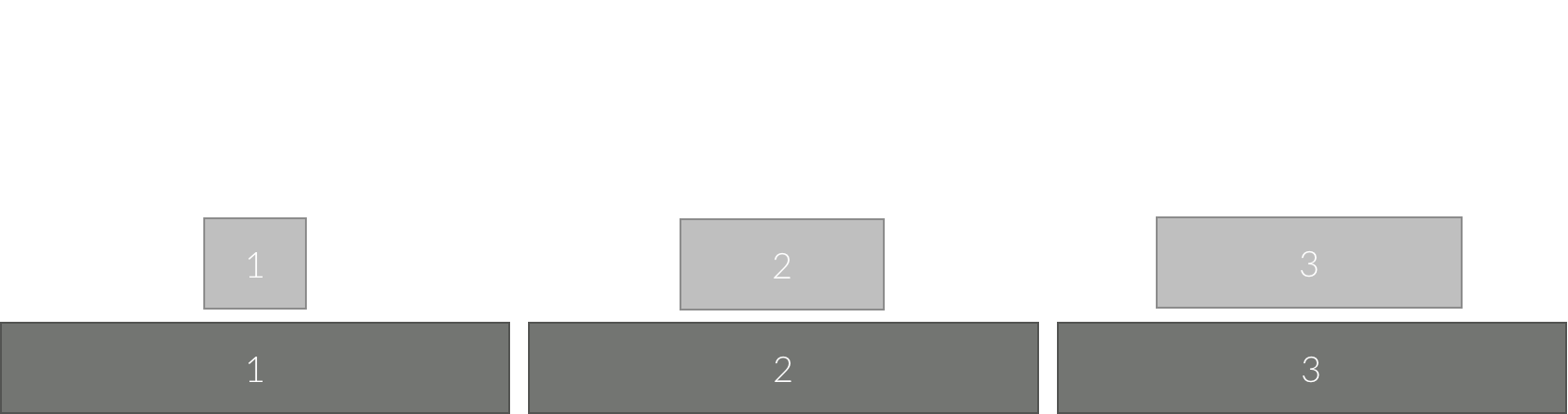
원판 2를 옮기기 전에 그 위에 있는 원판 1을 다른 곳으로 옮겨야 한다. 원판 1을 장대 2에서 장대 1로 옮겼다. (장대 3은 원판 2의 목표지점이므로)

원판 2를 장대 2에서 장대 3으로 옮겼다.

원판 1을 장대 1에서 장대 3으로 옮김으로써 모든 원판을 장대 3으로 옮겼다. 4번째 이동(원판 3을 장대 1에서 3으로 옮기는 이동) 이후 장대 2에 쌓여있는원판 1,2를 장대 3으로 옮기는 작업을 한것이다.

즉 원판 1~3을 장대 1에서 3으로 이동시키기 위해 한 작업은 다음 순서와 같다.

1. 원판 1~2를 장대 1에서 2로 이동시킨다. 1) 원판 1을 장대 1에서 3으로 이동 2) 원판 2를 장대 1에서 2로 이동 3) 원판 1을 장대 3에서 2로 이동
2. 원판 3을 장대 1에서 3으로 이동시킨다.
3. 원판 1~2를 장대 2에서 3으로 이동시킨다. 1) 원판 1을 장대 2에서 1로 이동시킨다 2) 원판 2를 장대 2에서 3으로 이동시킨다. 3) 원판 1을 장대 1에서 2로 이동시킨다.

위와 같이 크게 3개의 작업으로 나눌 수 있으며, 원판 1~2를 옮기는 작업은 다시 3개로 나뉜다.

1-1. 원판 이동 횟수

이동 횟수에 대해서 조금 더 살펴보자.

1. 원판 1을 목표지점으로 옮기는 경우 당연히 1번에 가능하다.
2. 원판 2를 목표지점으로 옮기는 경우
   • 원판 2는 한번만 옮기면 되지만
   • 원판 1을 다른 공간에 옮겨놨다 다시 목표지점으로 옮겨야 하기 때문에 2배의 작업이 필요하다.
3. 원판 3을 목표지점으로 옮기는 경우
   • 원판 3은 한번만 옮기면 된다.
   • 원판 2는 원판 3을 옮기기 전후 한번씩 움직여야 한다. 원판 3의 두배인 두번.
   • 원판 1은 원판 2를 옮기기 전후 한번씩 움직여야 한다. 원판 2의 두배인 네번.

총 이동횟수가 2의 거듭제곱의 합이되고 있다.

• \(N=1\)일때, \(1\)
• \(N=2\)일때, \(1+2=2^2-1=3\)
• \(N=3\)일때, \(1+2+4=2^3-1=7\)

즉 이동 횟수는 \(2^N-1\) 회임을 ‘\(N\)‘만을 이용해 알아 낼 수 있다.

int N;
scanf("%d",&N);
printf("%d\n",((1<<N)-1));

2. 재귀 함수를 이용한 비슷한 패턴의 작업 처리

1. 원판 1~2를 장대 1에서 2로 이동시킨다.
2. 원판 3을 장대 1에서 3으로 이동시킨다.
3. 원판 1~2를 장대 2에서 3으로 이동시킨다.

앞서 고찰한 결과에서 하위 단계의 처리는 미루고 상위 단계 먼저 생각하자. n개가 순서대로 장대 from에 쌓여있을 때 이를 장대 to로 옮긴다고 일반화 해보자. 또한 이때, from도 to도 아닌 남은 장대를 tmp라 하겠다.

1. 원판 1~n-1을 장대 from에서 tmp로 이동시킨다.
2. 원판 n을 장대 from에서 to로 이동시킨다.
3. 원판 1~n-1을 장대 tmp에서 to로 이동시킨다.

꽤 그럴싸 해졌다. 그렇다면 원판 1~n을 from에서 to로 옮기는 작업을 하는 함수 hanoi는

void hanoi(int n,int from,int to,int tmp){
  if(n==1){
    printf("%d %d\n",from,to);
    return;
  }
  hanoi(n-1,from,tmp,to);
  printf("%d %d\n",from,to);
  hanoi(n-1,tmp,to,from);
}

와 같이 구현될 수 있다. n=1일때 원판 0을 다른 곳으로 옮겨놨다 다시 가져오는 일은 하지 않으므로 원판 1만 옮기는 이동을 표시하고 반환하여 재귀반복을 끝내도록 했다.

문제에서 요구한 출력은 장대 A에서 장대 B로 원판을 옮길때 A B만 한줄에 출력하길 요구했으니 옮기는 작업에는

printf("%d %d\n",from,to);

만 구현하였다.

3. 최종 코드

앞선 단계에서 구현한 것들을 종합해보았다. 험악한 수의 규모와 달리 단순히 구현된다.

#include <stdio.h>

void hanoi(int n,int from,int to,int tmp){
  if(n==1){
    printf("%d %d\n",from,to);
    return;
  }
  hanoi(n-1,from,tmp,to);
  printf("%d %d\n",from,to);
  hanoi(n-1,tmp,to,from);
}

int main(void){
  int N;
    
  scanf("%d",&N);
  printf("%d\n",((1<<N)-1));
  hanoi(N,1,3,2);
    
  return 0;
}

하지만 이동횟수가 \(2^N-1\) 회이므로 \(N\)이 증가할수록 기하급수적으로 출력량과 기하급수적으로 호출되는 함수의 오버헤드가 험악한 실행시간을 안겨주었다.

제출 소스 확인하기