[BOJ] 2751번: 수 정렬하기 2 (합병정렬)

문제 링크: https://www.acmicpc.net/problem/2751

2750번에서 범위와 숫자의 크기가 늘어났다.

입력

Line 1: 정수 \(N(1≤N≤1000000)\)이 주어진다.

Line 2~(N+1): 절대값이 \(1000000\)보다 작거나 같은 정수가 한 줄에 하나씩 주어진다. (중복 없음)

출력

첫째 줄부터 \(N\)개의 줄에 오름차순으로 정렬한 결과를 한 줄에 하나씩 출력한다.

C99로 구현하였다.

0. 거품정렬의 한계

-_-;; ~~그만 알아보자~~

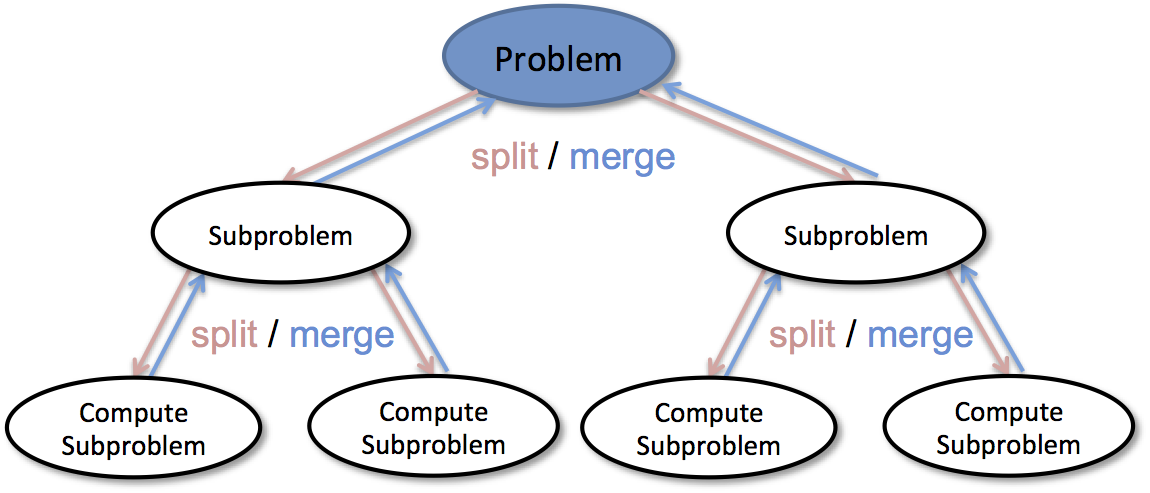
1. 분할 정복 (Divide and Conquer)

Divide_and_Conquer

void function(int* src, int begin, int end){
    if(end-begin<2) { /*Process something*/ return; }
    function(src,begin,(begin+end)/2);
    function(src,(begin+end)/2,end);
}

위 코드에서 볼 수 있듯, 분할 정복 알고리즘은 보통 재귀함수를 통해 구현된다. (함수 호출 오버헤드를 피하기위해 스택이나 큐 등의 자료구조를 사용할 수 있다.) 문제 상황 그대로는 해결이 어렵지만 분할한 케이스의 해결은 쉬울 때 이 알고리즘을 사용한다.

정렬을 할때 크기가 작을땐 비교하기 쉽지만, 크기가 커지면 복잡해지고 처리시간도 길어진다. 작은 케이스로 먼저 분할하고, 병합하면서 정렬하도록 하자. 이미 각자 정렬된 작은 리스트들을 다시 병합하면서 계속 정렬하는 과정을 거쳐야 하지만, 각 리스트들은 미리 정렬했기 때문에 비교 횟수를 줄일 수 있다.

사실 분할 및 정복은 위 함수를 그대로 차용할 수 있다. 문제는 분할된 작은 리스트들을 병합하면서 정렬을 동시해 구현해야한다. 예를 들어보자.

예시) \([2,5,4,3]\)

위 케이스는 sort함수의 재귀적 호출로

\[[2,5],[4,3]\]

로 2분할되고 결국,

\[[2],[5],[4],[3]\]

인 크기가 1인 리스트들로 다시 2분할된다. (정확히는 물리적으로 분할되는 것이 아니라 크기가 1인 리스트를 가리키는 함수들이 재귀호출에 의해 호출된다.)

이제 2분할된 리스트를 다시 병합하자. 2와 5는 순서대로이나, 4와 3은 역순이다. 순서를 바꾸면서 합병하면,

\[[2,5],[3,4]\]

와 같이 된다. 크기가 1일때는 비교하기도 뒤집기도 쉬웠지만 이젠 조금 복잡해졌다. \(2,3,4,5\) 순서가 되어야 하는데, 어떤 순서로 비교해야 할까. 다행히 리스트 내부 원소들은 정렬이 되어 있으므로 비교 순서는 index 순서대로 하면 될 것 같다.

void sort(int* src,int* dst,int begin,int end){
    int i,j,k;

    ...
  
    i=begin; j=(begin+end)/2;
    for(k=begin;k<end;++k)
    	dst[k] = (src[i]<src[j]) ? src[i++] : src[j++];

    memcpy(src+begin,dst+begin,(end-begin)*sizeof(int));
    // 합병 결과를 다시 원래의 데이터 저장공간으로 복사한다.
}

합병 전 두 리스트를 유지하는 상태에서 합병된 새 리스트를 만들어야 하기 때문에, dst를 도입하였다. dst라는 새로운 공간에 결과를 저장하고, 합병이 끝난 이후 따로 복사하기로 하자. 하지만 아직 문제가 남아 있다. 예시는 \([2,5],[3,4]\) 였지만, \([4,5],[2,3]\)의 경우에 허용된 index 범위 바깥을 접근하게 된다.

i=begin; j=middle;
for(k=begin;k<end;++k)
    dst[k] = (i<middle && (j>=end || src[i]<src[j]))
    	? src[i++] : src[j++];

i가 middle를 초과하면 무조건 i를 통한 참조를 중단하고 j가 가리키는 리스트만 참조해야하고 j가 end이상이 되면 j를 통한 참조를 중단하고 i가 가리키는 리스트만 참조해야 한다.

\[[2,3,4,5]\]

덕분에 분할되었던 리스트들이 병합되면서 정렬까지 되었다!

2. Merge Sort : 합병정렬 (병합정렬)

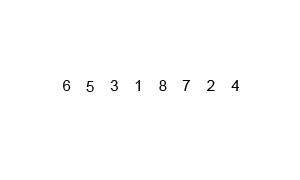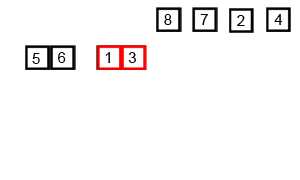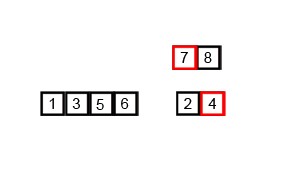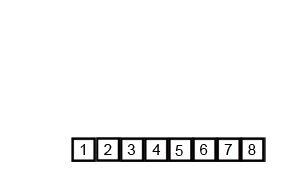
Merge_Sort

void mergeSort(int* src,int* dst,int begin,int end){
  int middle,i,j,k;
  if(end-begin<2) return;
    
  middle = (begin+end)/2;
  mergeSort(src,dst,begin,middle);
  mergeSort(src,dst,middle,end);
  
  i=begin; j=middle;
  for(k=begin;k<end;++k)
    dst[k] = (i<middle && (j>=end || src[i]<src[j]))
      ? src[i++] : src[j++];
      
  memcpy(src+begin,dst+begin,(end-begin)*sizeof(int));
}

나무위키: 병합정렬/합병정렬 (Merge Sort)

개발자는 존 폰 노이만으로 원소 개수가 1 또는 0이 될 때까지 두 부분으로 쪼개고 쪼개서 자른 순서의 역순으로 크기를 비교해 병합해 나간다. 병합된 부분 안은 이미 정렬되어 있으므로 전부 비교하지 않아도 제자리를 찾을 수 있다. 대표적인 분할 정복 알고리즘으로 존 폰 노이만의 천재성을 엿볼 수 있는 알고리즘이다.

성능은 아래의 퀵 정렬보다 전반적으로 뒤떨어지고, 데이터 크기만한 메모리가 더 필요하지만 최대의 장점은 데이터의 상태에 별 영향을 받지 않는다는 점’이다. 힙이나 퀵의 경우에는 배열 A[25]=100, A[33]=100인 정수형 배열을 정렬한다고 할 때, 33번째에 있던 100이 25번째에 있던 100보다 앞으로 오는 경우가 생길 수 있다. 그에 반해서 병합정렬은 이런 일이 발생하지 않는다. 기본적으로 병합정렬은 쪼겐 후 두 값을 비교할 때 값이 같으면 정렬하지 않게 설계되기 때문이다.

Quick Sort에 비해 다소 느리고, 앞서 dst를 도입했듯 메모리도 더 필요하지만, 안정정렬이며 퀵정렬과 다르게 데이터 상태에 따른 시간복잡도의 영향이 크지 않다.

3. 입출력 및 데이터 저장

int main(void){
  int N,i,*src, *dst;
  
  scanf("%d",&N);
  src=malloc(N*sizeof(int));
  dst=malloc(N*sizeof(int));
  
  for(i=0;i<N;++i)
    scanf("%d",src+i);
  
  mergeSort(src,dst,0,N);
  for(i=0;i<N;++i)
    printf("%d\n",src[i]);
  
  free(src); free(dst);
  return 0;
}

src외에도 dst가 필요하다는 점 이외에 특별한 건 없다.

4. 최종 코드

#include <stdio.h>
#include <malloc.h>
#include <memory.h>

void mergeSort(int* src,int* dst,int begin,int end){
  int middle,i,j,k;
  if(end-begin<2) return;
    
  middle = (begin+end)/2;
  mergeSort(src,dst,begin,middle);
  mergeSort(src,dst,middle,end);
  
  i=begin; j=middle;
  for(k=begin;k<end;++k)
    dst[k] = (i<middle && (j>=end || src[i]<src[j]))
      ? src[i++] : src[j++];

  memcpy(src+begin,dst+begin,(end-begin)*sizeof(int));
}

int main(void){
  int N,i,*src, *dst;
  
  scanf("%d",&N);
  src=malloc(N*sizeof(int));
  dst=malloc(N*sizeof(int));
  
  for(i=0;i<N;++i)
    scanf("%d",src+i);
  
  mergeSort(src,dst,0,N);
  for(i=0;i<N;++i)
    printf("%d\n",src[i]);
  
  free(src); free(dst);
  return 0;
}

결과	메모리	시간	코드 길이
맞았습니다!!	8932KB	436ms	725B

5. 재귀함수 호출을 쓰지 않은 합병정렬

C11로 구현하였다.

#include <stdio.h>
#include <malloc.h>
#include <memory.h>

void merge(int* fbegin, int* fend, int* sbegin, int* send, int* dst){
  while (fbegin != fend && sbegin != send)
    *dst++ = (*fbegin<*sbegin) ? *fbegin++ : *sbegin++;

  if (fbegin != fend) memcpy(dst, fbegin, (fend-fbegin)*sizeof(int));
  if (sbegin != send) memcpy(dst, sbegin, (send-sbegin)*sizeof(int));
}

void msort(int* base, int size) {
  int *src = (int*)base;
  int *dst = (int*)calloc(size, sizeof(int));
  for(int part=1; part<size; part<<=1){
    for(int idx=0;idx<size;idx+=(part<<1)){
      int fSiz=part, sSiz=part;
      if(size-idx<part*2){
        if(size-idx<part){
          fSiz=size-idx;
          sSiz=0;
        }
        else
          sSiz=size-(idx+part);
      }
      merge(src+idx, src+idx+fSiz, src+idx+part, src+idx+part+sSiz, dst+idx);
    }
    int *pt=src; src=dst; dst=pt;
  }

  if(src!=base){
    memcpy(base, src, size*sizeof(int));
    free(src);
  } else free(dst);
}

int main(void){
  int N,*array;
  
  scanf("%d",&N);
  array=malloc(N*sizeof(int));
  
  for(int i=0;i<N;++i)
    scanf("%d",array+i);
  
  msort(array,N);
  for(int i=0;i<N;++i)
    printf("%d\n",array[i]);
  
  free(array);
  return 0;
}

블로그 글을 참고~~베끼다시피~~했다.

결과	메모리	시간	코드 길이
`맞았습니다!!`	8932KB	440ms	1212B

제출 소스

하지만 별 도움이 안 됐다. 여전히 merge함수를 호출해서 그런가. 그래도 맞은사람을 보면 갖가지 최적화로 떡칠을 하거나 과감히 카운팅정렬을 해서 시간을 줄여놨다. 뭐…

PREVIOUS2750번: 수 정렬하기 (거품정렬)

NEXT11650번: 좌표 정렬하기