문제 링크: https://www.acmicpc.net/problem/11650

문제 상황

문제의 입력으로 주어질 2차원 좌표 순서쌍에 대해, 두 좌표의 대소를 다음과 같이 정의한다.

• \(x\)좌표가 더 큰 경우 해당 좌표가 더 크다.
• \(x\)좌표가 같은 경우, \(y\)좌표가 더 큰 좌표가 더 크다.
• \(x\)좌표와 \(y\)좌표가 모두 같은 경우 두 좌표의 크기는 같다.

입력되는 좌표들을 오름차순으로 정렬하시오.

입력

Line 1: 점의 개수 \(N (1 ≤ N ≤ 100,000)\)

Line 2~(N+1): \(i\)번째 좌표의 \(x\)성분, \(y\)성분인 \(x_i\)와 \(y_i\).

\((-100,000 ≤ x_i, y_i ≤ 100,000)\)이며, 좌표는 항상 정수이고 위치가 같은 두 점은 없다.

출력

오름차순으로 정렬된 순서대로 한줄에 한 좌표씩 출력한다.

C99로 구현하였다.

1. 좌표의 구현

1.1 좌표 데이터 저장

기본적으로 x라는 이름의 배열과 y라는 이름의 배열에 각각 좌표정보를 저장했다가 인덱스를 통해 참조하는 방식을 생각해 볼 수 있다.

int x[100000],y[100000];

...

printf("2번째 좌표: %d %d\n",x[2],y[2]);

뭐 이정도 수준에서는 그닥 불편함을 못 느끼지만 정렬과 같이 읽고 쓰고 옮기는 작업이 빈번하기 일어날 때는 이야기가 달라진다. 통일성도 떨어지고 판별 후 x배열, y배열의 교환작업을 따로따로 작업해야 한다. 둘을 묶을 수 있으면 좋을텐데…

int pos[100000][2];

...

printf("2번째 좌표: %d %d\n",pos[2][0],pos[2][1]);

좌표 하나를 크기 2의 배열로 저장하여 2차원 배열을 만들면 가능하다. 하지만 가독성을 위해 아래와 같이 구조체를 쓰겠다. 접근 방식이 좀 달라질뿐 복잡도나 알고리즘에 크게 영향을 미치지 않는다.

typedef struct{ int x,y; } coordinate;

int main(void){
  coordinate array[100000];
  
  ...
  
  printf("2번째 좌표: %d %d\n",array[2].x,array[2].y);
}

1.2 대소비교

정렬은 기본적으로 원소의 대소를 비교하여 순서대로 나열하는 작업이다. 앞서 좌표를 구현하였으니 구현된 좌표의 대소 비교를 정의하자.

가령 C++에서 위와 같은 좌표를 클래스로 정의하였다면,

bool operator<(coordinate& other) const{
    if(this->x==other.x)
    	return (this->y>other.y);
    return (this->x>other.x);
}

위와 같이 Operator Overloading을 하고 STL algorithm 함수를 쓰면 금방 해결된다. compare 함수를 sort함수의 인자로 주지 않으면 std::less를 기본 값으로 사용하기 때문이다. (같은 로직으로 compare 함수를 작성해 전달해도 된다)

(문제에서 같은 좌표는 없다는 조건을 걸었기 때문에 같은 경우는 고려하지 않았다.)

한편 C에 내장된 qsort 함수의 원형은 아래와 같다.

void qsort(void *_Base, size_t _NumOfElements, size_t _SizeOfElements, int (*_PtFuncCompare)(void const *, void const *));

마지막 인자는 함수포인터로 대소비교 후 크면 1, 같으면 0, 작으면 -1을 반환하는 함수(마치 strcmp처럼)를 정의 후 그 함수의 이름(함수의 메모리주소)를 전달해주면 된다. 우리도 이런 함수를 만들어보자.

int compare(const coordinate* const a, const coordinate* const b){
    if(a->x==b->x)
    	return (a->y>b->y ? 1 : (a->y==b->y ? 0 :-1));
    else
    	return (a->x>b->x ? 1 : -1);
}

식은 사실 위에서 이미 구현을 해서 compare함수 형태만 구현하면 됐다. 이제 compare 함수에 비교할 두 대상의 메모리주소 값을 전달하면 앞의 대상이 큰지(1), 작은지(-1) 반환해 줄 것이다. (Quick Sort를 이용할 예정이기 때문에 같은 경우도 처리해주었다.)

qsort(array,N,sizeof(int),compare);

2. Quick Sort : 빠른 정렬

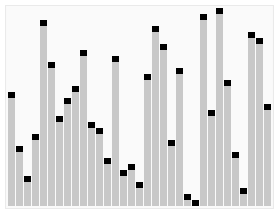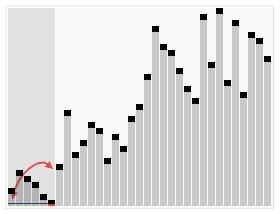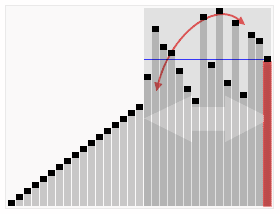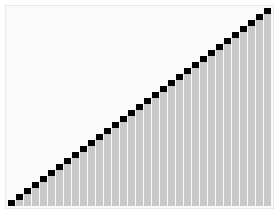
나무위키: 정렬 알고리즘 - 퀵 정렬(Quick Sort)

찰스 앤터니 리처드 호어가 1959년에 개발한 알고리즘이다. 퀵이라는 이름에서 알 수 있듯이 평균적인 상황에서 최고의 성능을 나타낸다. 컴퓨터로 가장 많이 구현된 정렬 알고리즘 중 하나이다. C, C++, PHP등의 언어에서 제공하는 정렬 함수에서 퀵 정렬 혹은 퀵 정렬의 변형 알고리즘을 사용한다. 방식은 적절한 원소 하나를 기준(피벗, pivot)으로 삼아 그보다 작은 것을 앞으로 빼내고 그 뒤에 피벗을 옮겨 피벗보다 작은 것, 큰 것으로 나눈뒤 나누어진 각각에서 다시 피벗을 잡고 정렬해서 각각의 크기가 0이나 1이 될 때까지 정렬한다. 이렇게 피벗을 잡고 이보다 작은 원소들을 왼쪽으로, 보다 큰 원소들을 오른쪽으로 나누는걸 partition step이라 한다. 퀵 정렬에도 이 partition step을 어떻게 하느냐에 따라 바리에이션이 매우 많으며, 성능 차이도 날 수 있다.

조금만 긁어온다는게 내가 하고 싶은 말을 여기서 다 해버려서 내가 할 말이 없다. 어쨌든, 한번 직접 구현해보자.

무조건 배열의 위치상 중간에 있는걸 피벗으로 잡거나 배열 중에 3개나 9개의 원소를 골라서 이들의 중앙값을 피벗으로 고르는 것이다. 이 방법을 사용하더라도 최악의 경우가 나올 수는 있지만 그 경우가 극히 드물게 된다. 다만 배열이 단순하게 비교 가능한 숫자가 아니라면 중앙값 피벗 방법이 비효율적일 수도 있다. 예를 들어서 비교하는데 연산이 아주 많이 들어가는 객체 또는 데이터 베이스. 이럴땐 그냥 무작위 또는 중간에 있는 원소를 피벗으로 잡는게 낫다.

비교연산이 아주 많은 객체에 해당하진 않지만 그냥 무난하게 중위값을 pivot으로 고르기로 하였다. 이후 위에서 언급하였듯, pivot값과 모든 값들을 비교하며 partition step을 진행한다. 그럼 pivot값을 기준으로 왼쪽은 모두 pivot값보다 작고, 오른쪽은 모두 pivot값보다 큼이 보장된다. 역시 분할정복으로 마무리 해주면 될 것 같다.

void quickSort(coordinate *array, int left, int right){
    int pivotIndex;
    coordinate pivot = array[(left+right)/2];
    
    /*partition step: pivot과 비교하여 작으면 왼쪽, 크면 오른쪽으로 보내는 작업*/
	
    if(pivotIndex-left>1) quickSort(array,left,pivotIndex-1);
    if(right-pivotIndex>1) quickSort(array,pivotIndex+1,right);
}

이제 partition step 작업을 할 차례이다. 여러가지 방법이 있지만 현재 목표는 pivot보다 큰지 작은지 분류하는 것뿐이니 간단하게 구현해보자.

int i=left, j=right;
while(i<=j){
    while(compare(&pivot,array+i)==1) ++i;
    while(compare(array+j,&pivot)==1) --j;
    if(i<=j){
        tmp=array[i];
        array[i]=array[j];
        array[j]=tmp;
        ++i; --j;
    }
}

작으면 왼쪽, 크면 오른쪽에 놓아야 하니 각각 왼쪽, 오른쪽부터 탐색해나갈 index i, j를 사용했다. 왼쪽에서는 pivot보다 큰 값을, 오른쪽에서는 pivot보다 작은 값을 찾을 때까지 탐색하고, 두 원소는 각각 반대쪽으로 이동시켜야 하므로, 교환하였다. 이러한 과정을 i<=j인 동안 계속 반복한다. i와 j가 교차됐음은 모두 이미 pivot까지 탐색을 마치고 pivot을 지나쳐 서로 반대편에 진입한 것이므로 반복문을 탈출한다.

void quickSort(coordinate *array, int left, int right){
    int i=left,j=right;
    coordinate tmp, pivot = array[(left+right)/2];
    
    while(i<=j){
    	while(compare(&pivot,array+i)==1) ++i;
        while(compare(array+j,&pivot)==1) --j;
        if(i<=j){
            tmp=array[i];
            array[i]=array[j];
            array[j]=tmp;
            ++i; --j;
        }
    }
    
    if(j>left) quickSort(array,left,j);
    if(right>i) quickSort(array,i,right);
}

이를 종합하면 위와 같다. 위 반복문을 탈출하면 j는 pivot 바로 전, i는 pivot 바로 이후로 오기 때문에 pivotIndex를 쓰지 않고, i,j를 재활용했다.

3. 최종 코드

#include <stdio.h>
#include <malloc.h>

typedef struct{ int x,y; } coordinate;

int compare(const coordinate* const a, const coordinate* const b){
    if(a->x==b->x)
    	return (a->y>b->y ? 1 : (a->y==b->y ? 0 :-1));
    else
    	return (a->x>b->x ? 1 : -1);
}

void quickSort(coordinate *array, int left, int right){
    int i=left,j=right;
    coordinate tmp, pivot = array[(left+right)/2];
    
    while(i<=j){
    	while(compare(&pivot,array+i)==1) ++i;
        while(compare(array+j,&pivot)==1) --j;
        if(i<=j){
            tmp=array[i];
            array[i]=array[j];
            array[j]=tmp;
            ++i; --j;
        }
    }
	
    if(j>left) quickSort(array,left,j);
    if(right>i) quickSort(array,i,right);
}

int main(void){
    int N,i;
    coordinate* array;
    
    scanf("%d",&N);
    array=malloc(N*sizeof(coordinate));
    for(i=0;i<N;++i)
    	scanf("%d %d",&(array[i].x),&(array[i].y));
    
    quickSort(array,0,N-1);
    
    for(i=0;i<N;++i)
    	printf("%d %d\n",array[i].x,array[i].y);
    
    free(array);
    return 0;
}

제출 소스 확인하기