이 글은 EBS 수학과 함께하는 AI 기초를 바탕으로 작성되었습니다.
글 발췌나 라이선스에 관련한 안내를 찾아볼 수 없었지만 아무리 무료로 배포된다하더라도 엄연한 출판물이므로 교재 내용을 막 퍼오기는 어렵다고 판단하였다.
사실 교재 내용도 꽤 친절하여 내가 뭐 기록을 남길만한 부분도 많지 않다. 다만 알게된 내용 몇가지를 정리하거나, 제공된 소스를 일부 바꾸어 보는 것도 괜찮을 듯하여 글로 남기고자 한다.
1. 인공지능 소프트웨어와 대화하는 취미를 가진 태희
이번 단원에선 태희가 인공지는 소프트웨어와 대화를 하다가 소리 데이터를 어떻게 저장, 처리하고 인식하는 지가 궁금해졌다.
아니 그럼 바이너리 파일을 직접 까보렴.
2. 소리 데이터 표현하기
교재에서는 먼저 음파가 어떤 것인지부터 다룬다. 뭐 다 아는 부분이니 길게 설명할 필요야 없겠다만 당연하고 중요한 부분만 짚고 넘어가자.
우리가 보통 sine파처럼 시각화해서 보는 파동은 파동의 진행방향과 매질의 진동방향이 수직인 횡파이다. 그러나 음파는 종파이다.
그러면 그동안 종파인 음파를 어떻게 횡파로 시각화 한걸까. 간단하게 음파에 의해 진동하는 매질의 시간에 따른 변위를 시각화 한것이라 보면 되겠다.
근데 음파든 뭐 매질의 변위이든 위상의 변화이든 결국 연속적인 아날로그 데이터다. ADC에서는 이를 매우 짧은 시간구간으로 쪼개는 표본화, 샘플링 작업을 통해 이산적인 구간들로 만들고, 이 진폭값을 데이터 범위에 맞는 디지털값으로 변환하는 양자화를 진행해 디지털 데이터로 변환 할 것이다.
이번단원에서는 무손실 무압축의 소리데이터가 그대로 저장된 가장 편집이 쉬운 wav 파일 포맷을 이용했다.
2-1. 임의 Signal 생성하기
wav파일도 파일헤더와 wav포맷 헤더를 가지겠다만 그건 우리의 강력한 파이썬 라이브러리가 해결해줄테니 안심하자.
어쨌든 결국 우리는 raw data만 처리하면 되고, raw data는 결국 \(\frac{1}{samplerate}\) 초 당 진폭을 표현한게 다 아닌가. 쉽게 신호를 만들어 볼 수 있겠다.
가장 기본 진동이라 여겨지는 sin 함수의 값을 raw data로 저장하면 기계음처럼 “삐-“ 소리로 들리는 음압시계열이 완성된다. 한번 만들어 보자.
import numpy as np
import sounddevice as sd
rate = 44100.0 # SampleRate, 44100 Sampling per 1 sec, 44100Hz
sec = 1 # Signal Duration: 1 sec
t = np.arange(0, sec, 1/rate) # Time array contains range of [0:1]
# unit time: 1/rate
# Signal 생성하기
sin_freq = 440 # Frequency for sine func
signal1 = np.sin(2*np.pi*sin_freq*t ) # get sine value from radian converted from timestamp
sd.play(signal1,rate)
sounddevice.play는 samplerate와 ndarray형태의 음압시계열을 입력받아 직접 사운드 출력 장치를 통해 출력시킨다. 실행해보면 \(A_4\) 음(\(440Hz\))의 Singletone을 듣게 된다.
2-2. 임의 Noise 생성하기
이번엔 노이즈를 만들어 보겠다. 학교 교실에 있는 TV의 채널을 돌리다 유효하지 않은 채널에 접속하면 노이즈 화면과 함께 1초뒤 우리들의 귀를 폭발시켰던 그 치지직 소리 말이다… 꼭 그런 채널만 골라서 트는 X맨이 반마다 한 명씩 있다.
noise = np.random.uniform(-0.3, 0.3, len(t)) # Uniform Distribution Random
# In range of -0.3~0.3 (30% volume of signal)
sd.play(noise,rate)
다시 느끼지만 NumPy는 강력하다. 무려 균등분포 난수도 생성해준다. 친절히 범위와 길이까지 설정가능하다.
2-3. 소리 합성하기
signal에 들어있는 데이터에 주목해라. 결국 numpy.ndarray에 담겨있는 행렬이다. 선형성을 가진다. 더하고 빼고 스칼라배 곱하고 지지고 볶아도 된다!! 그러니 앞서 만든 신호들을 합쳐보자.
signal1 = np.sin(2*np.pi*sin_freq*t ) # get sine value from radian converted from timestamp
signal2 = np.sin(2*np.pi*sin_freq*2*t ) # 1 Octave higher signal (Double times freq)
noise = np.random.uniform(-0.3, 0.3, len(t)) # Uniform Distribution Random
# In range of -0.3~0.3 (30% volume of signal)
mixed = 0.5*(signal1 + signal2) + noise # Mixing signals with noise
sd.play(mixed,rate)
뭐 어차피 이따 조정할 거니 상관 없지만 -1~1 범위 형식을 유지하도록 적절히 배율을 곱한채 싹 다 더했다. Noise를 더하긴 했지만 singletone은 너무 밋밋하다 싶어 한 옥타브 높은 \(A_5\) 음(\(880Hz\))도 추가하였다.
들어보면 오묘하게 불쾌하다. (?)
2-4. Fourier Transform
사실 벌써부터 나오나 하는 감이 없지 않아 있지만, 어차피 직접 계산하는게 아니라 우리의 든든한 NumPy가 해결해주기 때문에 우리가 할일은 그저 numpy.fft 라이브러리의 함수들에 적절한 값을 인자로 던저주는 일 뿐이니 걱정하지 않아도 되겠다.
함수 \(h : \mathbb{R} \to \mathbb{C}\)에 대해 아래와 같이 \(\hat{h}=F[h]: \mathbb{R} \to \mathbb{C}\)를 정의한다.
\[\hat{h}(t)=F[h](t)\equiv\int^{\infty}_{-\infty} e^{-2 \pi itx}h(x)dx \ \ \ \ \ (i=\sqrt{-1})\]이 때 변환 \(F[h]\)를 함수 \(h\)의 푸리에 변환으로 정의하더라…
이게 뭐하는 적분변환인가 싶지만 푸리에 변환을 통해 도대체 규칙성, 주기라고는 찾아볼 수 없는 함수를 각각의 정현파들로 분리해낸다. 진짜 처음 푸리에 변환을 접했을때 그 험악하게 생긴 식들과 화려한 결과들에 당혹감을 금치 못했었다…
어쨌든 푸리에 변환을 통해 각 주파수대역별로 정현파를 분리해내니, 주파수에 기반한 신호분석이 용이해진다. time domain에서 꽁꽁 숨어있던 주파수가 frequency domain에서 그냥 떡하니 드러나니 진짜 눈물이 난다.
뭐 저 위의 식은 어디까지나 가장 기본적인 수학적 정의이다. 하지만 우리는 이산적인 데이터를 다뤄야 하기 때문에 이산 푸리에 변환을 써야하겠다. numpy.fft는 고속 푸리에 변환 알고리즘을 통해 이산 푸리에 변환을 하는 라이브러리이며, 아래와 같이 사용할 수 있다.
freq = np.fft.fftfreq(len(t), 1/rate) # fftfreq returns axis array for Fourier Transformed
fourier = np.fft.fft(mixed) # get fourier transformed value
fourier변수에는 푸리에 변환을 거친 mixed가 들어간 것이어서 다른 설명이 필요 없고, 특이하게도 numpy.fft는 fftfreq함수를 제공한다. 다름아닌 기존 time domain t에 대응하는 frequency domain이다. 정말 파이썬은 다 떠먹여준다…
2-5. Filtering
앞서 살펴본 강력한 기능들 덕분에 별의별 장난을 다 할 수 있게되었다. 때문에 소꿉장난을 해보고자 한다.
fourier_filtered = np.array(fourier) # new ndarray for filtered fourier transformed
for i in range(len(fourier)): # iterate in range of all freq
if(np.abs(fourier[i])<1000): # if signal in specific freq is too weak,
fourier_filtered[i]=complex(1e-1,0) # disregard. (give enough small complex value)
mixed_filtered = np.fft.ifft(fourier_filtered).real # get filtered wave (take only real part)
sd.play(mixed_filtered,rate)
푸리에 변환후, 모든 주파수 대역을 손수 탐색하며 잔챙이들을 죽이고 있다! 앞서 noise는 volume을 30%로 축소시켜 합성하였기 때문에 noise는 필터링 될 것이다.
앞서살펴본 푸리에 변환 정의식에서 볼 수 있듯, 치역은 복소수이며, 차마 0을 값으로 줄 수 없어 (log로 스케일을 줄일 예정이다.) 저런 애매한 값으로 대치하였다.
이제 numpy.fft.ifft를 통해 푸리에 역변환으로 다시 음압시계열 형태로 돌려놓는다.
2-6. 2-3-10.py
앞서 다룬 것들을 전부 하나로 합쳐보자. (sounddevice를 릴리즈 하는 문제로 소리를 출력하는 부분은 마지막에 몰아넣었다. 자세한건 2-3-10.py 참조.)
# 전략 (2-1 ~ 2-5 참고)
t_range = 200 # range of time to plot
freq_start = 200
freq_stop = 1000
plt.subplot(331)
plt.title("440Hz - Singletone")
plt.ylim(-1, 1)
plt.plot(t[:t_range], signal1[:t_range], color = 'blue')
plt.subplot(332)
plt.title("880Hz - Singletone")
plt.ylim(-1, 1)
plt.plot(t[:t_range], signal2[:t_range], color = 'blue')
plt.subplot(333)
plt.title("Noise")
plt.ylim(-1, 1)
plt.plot(t[:t_range], noise[:t_range], color = 'red')
plt.subplot(323)
plt.title("Mixed - Dualtone with noise")
plt.plot(t[:t_range], mixed[:t_range], color = 'orange')
plt.subplot(324)
plt.title("Fourier Trasformed")
plt.plot(freq[freq_start:freq_stop], np.log10(np.abs(fourier[freq_start:freq_stop])), color='violet')
plt.subplot(325)
plt.title("Mixed - Filtered")
plt.plot(t[:t_range], mixed_filtered[:t_range], color = 'green')
plt.subplot(326)
plt.title("Fourier Trasformed - Filtered")
plt.plot(freq[freq_start:freq_stop], np.log10(np.abs(fourier_filtered[freq_start:freq_stop])), color='violet')
play = np.append(signal1,signal2,axis=0) # concatenating signals to play.
play = np.append(play,noise,axis=0) # concatenating noise to play.
play = np.append(play,mixed,axis=0) # concatenating result to play.
play = np.append(play,mixed_filtered,axis=0) # concatenating filtered to play.
sd.play(play,rate) # play through sounddevice
plt.show()
실행해보라. 괴상한 소리와 함께 아래와 같은 그래프덩어리들을 출력해 낼것이다.
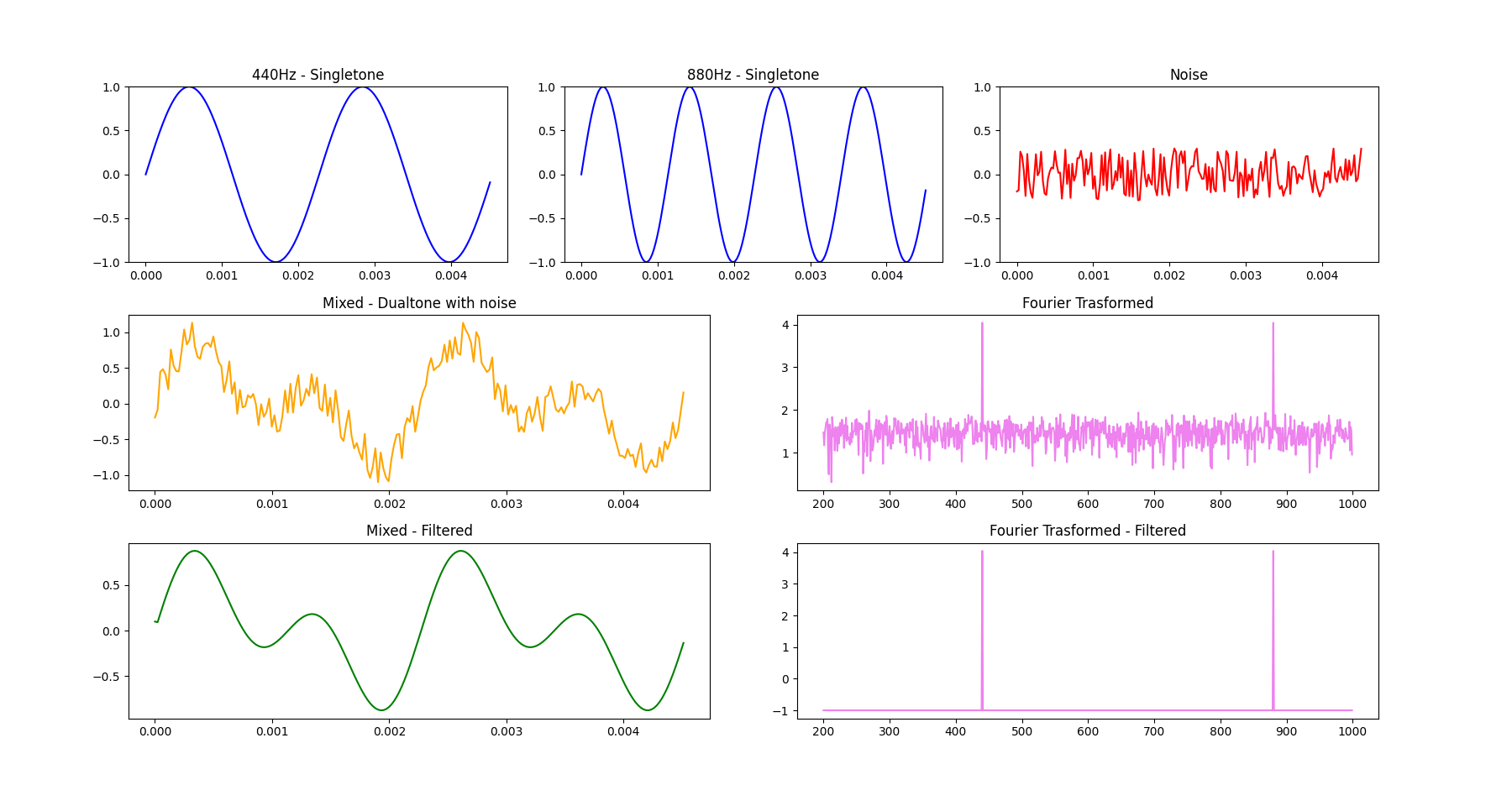
처음 1행의 소스 3개를 합성하여 2행의 음압시계열을 만들어 냈고, 푸리에 변환을 보면 원래 소스에 있던 Dualtone의 성분이 우람하게(?) 솟아나 있고 나머지 영역에 잔챙이들이 지저분하게 있는게 보인다.
앞서 2-5에서 필터링을 통해 잔챙이들을 제거해주고 다시 역변환을 통해 3행과 같은 깔끔한 음압시계열을 얻어낼 수 있었다.
3. 소리 데이터 파일 읽고 쓰기 powered by scipy.io.wavfile
이번 실습에 사용된 wav파일 샘플은 University of South Carolina의 John Burkardt의 개인자료실에서 가져왔습니다.
thermo.wav
Homer Simpson declares that "In this house, we obey the laws of thermodynamics!"
woman.wav
the opening bars of "American Woman" by The Guess Who
가져오긴 했는데… 이게 뭔가 싶다 ㅋㅋㅋㅋㅋ 도대체 Burkardt씨는 왜 저런걸 샘플로 썼을까…
3-1. wav file 읽기
scipy.io.wavfile에서 wav file의 읽기 및 쓰기를 지원한다.
import numpy as np
from scipy.io import wavfile
v_rate, v_data = wavfile.read('thermo.wav')
b_rate, b_data = wavfile.read('woman.wav')
간단히 위와 같이 읽힌다. wavfile.read에 wav파일 경로를 넘겨주면 wav파일의 samplerate와 음압시계열 raw data를 tuple형태로 반환한다.
3-2. Mixing
Mixing은 쉽다만 기본적으로 서로 다른 두 파일을 사용하는 것이기 때문에 형식이 같은지 확인하고 정규화가 필요하겠다.
print('voice and backgroud (rate, shape):',v_rate, v_data.shape,b_rate, b_data.shape)
if(len(v_data.shape)!=len(b_data.shape)): # if number of channel is not matched
# Unify to mono channel by taking mean between Left and Right Channel
if(len(v_data.shape)>1): # if it is stereo
v_data=np.array((v_data[:,0]+v_data[:,1])/2) # Mean
if(len(b_data.shape)>1): # if it is stereo
b_data=np.array((b_data[:,0]+b_data[:,1])/2) # Mean
# Down-Sampling
if (v_rate > b_rate) :
diffRate = v_rate // b_rate # get diff Multiple rate
v_data = np.array(v_data[0:len(v_data):diffRate]) # skip to match sample rate
rate = b_rate # dst sample rate
elif (v_rate < b_rate) :
diffRate = b_rate // v_rate
b_data = np.array(b_data[0:len(b_data):diffRate])
rate = v_rate
else :
rate = b_rate
print('voice and backgroud (rate, shape):',v_rate, v_data.shape,b_rate, b_data.shape)
# Normalize before processing
v_data = np.array(v_data/np.max(np.abs(v_data))) # normalize in range of [-1:1]
b_data = np.array(b_data/np.max(np.abs(b_data))) # normalize in range of [-1:1]
차례로 채널수가 다르면 Mono channel로 다운그레이드 하는 작업을 추가하였고, samplerate가 다를경우 높은 samplerate의 파일을 downsampling하는 작업을 추가하였다. 사실 예시로 가져온 파일들은 mono channel에 samplerate도 그닥 높지 않지만 같아서 별 문제가 안 되는 친구들이다.
근데 문제는 다른 곳에서 발생했다. thermo.wav가 8bit형식이었다. woman.wav는 16bit인데 말이다. 이왕 통일하는 거 -1 ~ 1 범위 안으로 들어오도록 정규화를 진행하였다.
# Insert and mix voice in background at 3 sec.
b_data[rate*3:rate*3+len(v_data)] *= 0.3
b_data[rate*3:rate*3+len(v_data)] += 0.7*v_data
Mixing은 간단하게 끝났다. 3초부터 thermo.wav의 시간만큼의 구간에 그냥 더해버렸다. 각각의 음량을 좀 조절하기 위해 가중치를 주었다.
3-3. wav file 쓰기
# Restore to 16bit wavfile (signed int16)
scaled = np.int16(b_data/np.max(np.abs(b_data)) * 32767)
wavfile.write('mixed.wav', rate, scaled)
뭐 16비트 wav파일로 쓰자. 사실 이미 정규화 되어 있고, 믹싱 과정에서도 비율을 유지하였기때문에 저 최댓값을 구해 나누는 과정은 사족에 가깝지만, 남겨두었다.
저 과정을 통해 -1 ~ 1 의 범위 내로 정규화 되고, 이에 0x7FFF를 곱하였다. 즉 범위를 \(-32768\) ~ \(32767\)로 둔 것이다. signed int16의 범위이다. 진폭이니 당연히 음의 값도 가지고 이에 따라 signed가 당연하다.
이후 wavfile.write에 새로 쓸 파일의 경로, 이름과 samplerate, 그리고 ndarray형태의 음압시계열을 넘겨주면 wav파일을 쓴다.
3-4. 2-3-11.py
mixed.wav
thermo.wav is inserted on woman.wav at 3 sec
with 70% of volume, while woman is decreased to 30%.
우스운 결과물이 나왔다. 소스 전체는 2-3-11.py를 참고하여라.
